Page 26 - Ικανότητες μαθητών Ε'-ΣΤ' Δημοτικού στα κλάσματα και επίλυση προβλήματος

Κατά τη μετάβαση από τη θεώρηση ενός ακέραιου αριθμού, στα κλάσματα, οι μαθητές

πρέπει να αναπτύξουν μεγάλη κατανόηση των πολλαπλών κατασκευών των κλασμάτων. Χωρίς
αυτή, οι μαθητές δεν είναι δυνατό να καταλάβουν τις πιθανές σημασίες του αριθμητή και του

παρονομαστή καθώς επίσης και των διαφορών μεταξύ τους (Empson & Levi, 2011; Petit et al,

2010; Jigyel et al, 2007). Για παράδειγμα, όταν θεωρούμε το κλάσμα ως σχέση μέρους – όλου, ο
αριθμητής αντιπροσωπεύει την αρίθμηση των κομματιών στα οποία έχει χωριστεί το όλο, και ο

παρονομαστής αντιπροσωπεύει τη μονάδα. Όταν θεωρούμε ένα κλάσμα σαν πηλίκο, ο αριθμητής
είναι μια ποσότητα (διαιρετέος) που διαιρείται από τον παρονομαστή (διαιρέτης). Οι μαθητές,

πρέπει επίσης να κατανοήσουν ότι ο αριθμητής και ο παρονομαστής έχουν διαφορετικούς ρόλους
στο κλάσμα, και οι διαφορετικές αναπαραστάσεις αυτού, εξαρτώνται από τον ρόλο τους. Για

παράδειγμα, στη σύγκριση των κλασμάτων, αν οι μαθητές δεν καταλαβαίνουν ότι ο ρόλος του

αριθμητή είναι διαφορετικός από τον ρόλο του παρονομαστή, τότε δυσκολεύονται με τις ακόλουθες
παραστάσεις 3/4>3/6 και 3/4>1/4. Στην πρώτη παράσταση, το κλάσμα με τον μικρότερο

παρονομαστή (4) αντιπροσωπεύει ένα μεγαλύτερο κλάσμα αφού τα κομμάτια είναι μεγαλύτερα,
ενώ στη δεύτερη παράσταση, το κλάσμα με τον μικρότερο αριθμητή (1) αντιπροσωπεύει ένα

μικρότερο κλάσμα καθώς τα κομμάτια έχουν το ίδιο μέγεθος (Behr et al., 1993).

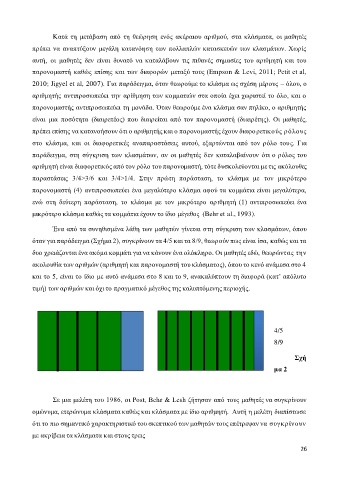
Ένα από τα συνηθισμένα λάθη των μαθητών γίνεται στη σύγκριση των κλασμάτων, όπου

όταν για παράδειγμα (Σχήμα 2), συγκρίνουν τα 4/5 και τα 8/9, θεωρούν πως είναι ίσα, καθώς και τα
δυο χρειάζονται ένα ακόμα κομμάτι για να κάνουν ένα ολόκληρο. Οι μαθητές εδώ, θεωρώντας την

ακολουθία των αριθμών (αριθμητή και παρονομαστή του κλάσματος), όπου το κενό ανάμεσα στο 4

και το 5, είναι το ίδιο με αυτό ανάμεσα στο 8 και το 9, ανακαλύπτουν τη διαφορά (κατ’ απόλυτο
τιμή) των αριθμών και όχι το πραγματικό μέγεθος της καλυπτόμενης περιοχής.

4/5
8/9

Σχή
μα 2

Σε μια μελέτη του 1986, οι Post, Behr & Lesh ζήτησαν από τους μαθητές να συγκρίνουν
ομώνυμα, ετερώνυμα κλάσματα καθώς και κλάσματα με ίδιο αριθμητή. Αυτή η μελέτη διαπίστωσε

ότι το πιο σημαντικό χαρακτηριστικό του σκεπτικού των μαθητών τους επέτρεψαν να συγκρίνουν
με ακρίβεια τα κλάσματα και στους τρεις

26